elliptica

attractors

In the mathematics of dynamical systems, an attractor is a set of values towards which a system naturally evolves over time, effectively acting like a "magnet" for the system's behaviour.

System: Chaos Theory (Continuous ODE)
Name: Arneodo Attractor
Color Map: winter (Mapped to Z-Coordinate)
Coordinate System: 3D Phase Space (x, y, z)
Time Span: 200.0
Points: 50000
Equation: dx/dt=y; dy/dt=z; dz/dt=-alphax - betay - gamma*z + x^2
Parameters: alpha=7.5, beta=3.8, gamma=1.0

System: Chaos Theory (Continuous ODE)
Name: Rössler Attractor
Coordinate System: 3D Phase Space (x, y, z)
Time Span: 200.0
Points: 50000
Equation: dx/dt = -y-z; dy/dt = x+ay; dz/dt = b+z(x-c)
Parameters: a=0.2, b=0.2, c=5.7
Render Style: Scatter (s=0.5) with Transparent Background

System: Chaos Theory (Continuous ODE)
Name: Lorenz Attractor
Color: #ff006e (Pink)
Parameters: rho={RHO}, sigma={SIGMA}, beta={BETA:.4f}
Time Span: {T_END}
Points: {NUM_POINTS}
Render Style: Line Plot (lw=0.7) with Transparent Background

System: Chaos Theory (Continuous ODE)
Name: Aizawa Attractor
Color Map: viridis (Mapped to Z-Height)
Coordinate System: 3D Phase Space (x, y, z)
Time Span: 100
Points: 50000
Equation: dx/dt=(z-b)x-dy; dy/dt=dx+(z-b)y; dz/dt=c+az-z^3/3-(x^2+y^2)(1+ez)+fzx^3
Parameters: a=0.95, b=0.7, c=0.6, d=3.5, e=0.25, f=0.1

System: Chaos Theory (Continuous ODE)
Name: Chen Attractor
Color Map: plasma (Mapped to Z-Coordinate)
Coordinate System: 3D Phase Space (x, y, z)
Time Span: 50.0
Points: 50000
Equation: dx/dt=a(y-x); dy/dt=(c-a)x-xz+cy; dz/dt=xy-bz
Parameters: a=35.0, b=3.0, c=28.0

System: Chaos Theory (Continuous ODE)
Name: Sprott B Attractor
Color Map: cool (Mapped to Z-Coordinate)
Coordinate System: 3D Phase Space (x, y, z)
Time Span: 200.0
Points: 50000
Equation: dx/dt=ayz; dy/dt=x-z; dz/dt=b-xy
Parameters: a=0.4, b=1.2
Render Style: Scatter (s=0.5) with Transparent Background

parametric

Parametric curves are geometric shapes defined by equations where each coordinate is a function of a single independent variable (often "t"), allowing for the description of complex, self-intersecting paths that standard functions cannot model.

System: 2D Parametric Curve
Name: Temple H. Fay Butterfly Curve
Color Map: hsv (Cyclic, Mapped to Theta)
Coordinate System: Polar to Cartesian
Theta Range: 0 to 24pi
Data Points: 100000
Equation r: exp(sin(theta)) - 2cos(4theta) + sin((2theta - pi)/24)^5

System: 2D Parametric Curve
Name: Cochleoid Curve (Snail Curve)
Color Map: magma (Non-Cyclic, Mapped to Theta)
Coordinate System: Polar to Cartesian
Theta Range: -20pi to 20pi
Data Points: 100000
Equation r: a * sin(theta) / theta
Parameter a: 10.0

System: Maurer Rose (Parametric)
Name: Crystalline Rose
Coordinate System: 2D Polar -> Cartesian
Domain: k in [0, 360]
Parameter n: 6 (Petal Count/Frequency)
Parameter d: 71 (Angular Step in Degrees)
Equation: theta = k * d
r = sin(n * theta)
x = r * cos(theta)
y = r * sin(theta)

System: 2D Parametric Curve
Name: Hypotrochoid (Spirograph)
Coordinate System: Cartesian
Parameter t Range: 0 to 106*pi
Data Points: 100000
Equation x: (R - r) * cos(t) + d * cos((R - r) / r * t)
Equation y: (R - r) * sin(t) - d * sin((R - r) / r * t)
Parameters: R=300.0, r=53.0, d=90.0

System: 2D Parametric Curve
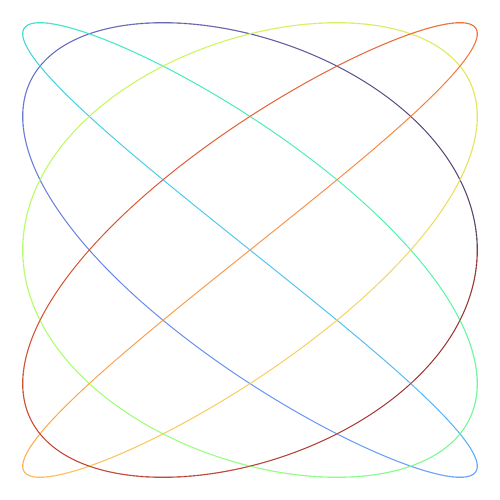Name: Lissajous Curve (5:4 Ratio)
Color Map: turbo (Cyclic, Mapped to Time Parameter t)
Coordinate System: Cartesian
Parameter t Range: 0 to 2pi
Data Points: 100000
Equation x: A * sin(at + delta)
Equation y: B * sin(b*t)
Parameters: A=10.0, B=10.0, a=5, b=4, delta=pi/2

System: Damped Parametric (Harmonograph)
Name: Wireframe Shell / Damped Lissajous
Coordinate System: Cartesian
Parameter t Range: 0 to 800pi
Data Points: 100000
Equation x: A * sin(f1t + delta) * exp(-d1t)
Equation y: B * sin(f2t) * exp(-d2*t)
Parameters: A=10.0, B=10.0, f1=3.0, f2=3.02, d1=0.002, d2=0.002, delta=pi/2

System: 2D Parametric Curve (Guilloché)
Name: Intricate Security Pattern Variation
Coordinate System: Cartesian
Parameter t Range: 0 to 200*pi
Data Points: 100000
Equation: Modulated Hypotrochoid (see code for full formulation)
Parameters: R=50.0, r=0.5, p=20.0, Q=8.0, m=10.0

System: 2D Parametric Curve
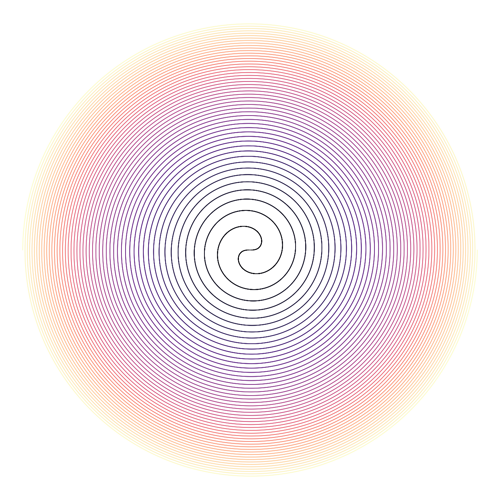Name: Fermat's Spiral (Parabolic Spiral)
Color Map: magma (Non-Cyclic, Mapped to Theta)
Theta Range: 0.0 to 50*pi
Data Points: 200000 (Two Arms)
Equation r: c * sqrt(theta)
Parameter c: 2.0

fractals

Fractals are infinitely complex patterns created by repeating a simple equation in a feedback loop, resulting in shapes that look the same at any scale (self-similarity).

System: 2D Fractal (Iterated Function System)
Name: Barnsley Fern
Color Map: viridis (Mapped to Y-coordinate)
Coordinate System: Cartesian (Iterative)
Points: 500000
Algorithm: Probabilistic Affine Transformations (4 rules)

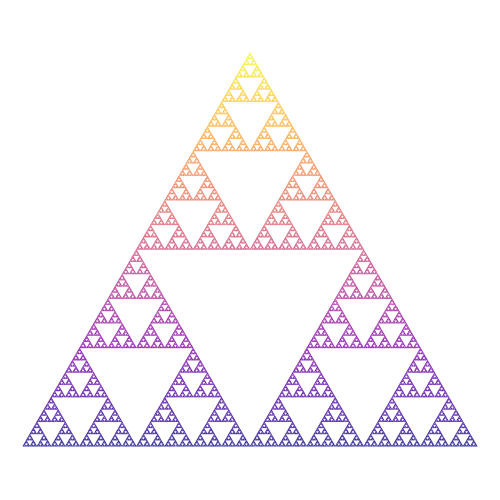System: 2D Fractal (Chaos Game)
Name: Sierpinski Triangle (Gasket)
Color Map: plasma (Mapped to Y-coordinate)
Coordinate System: Cartesian (Iterative)
Points: 500000
Algorithm: Chaos Game (3 vertices, 1/2 step)

System: 2D Fractal (Iterated Function System / L-System)
Name: Heighway Dragon Curve
Color Map: magma (Mapped to Path Index)
Coordinate System: Cartesian (Iterative)
Iterations: 18 (Batch Render), 16 (Viewer)
Algorithm: Iterative Folding Sequence

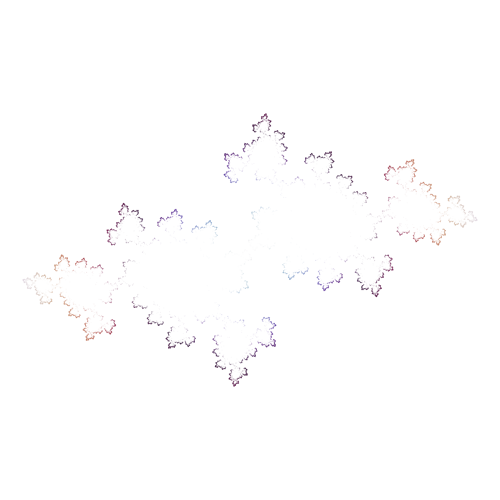System: 2D Fractal (Inverse Iteration Method)
Name: Julia Set Boundary
Color Map: twilight (Mapped to Radial Distance)
Coordinate System: Complex Plane (Cartesian)
Points: 1000000
Equation: z_next = +/- sqrt(z - c)
Parameter c: -0.70176 - 0.3842j

System: 2D Fractal (Geometric Recursion)
Name: Pythagoras Tree
Color Map: viridis (Mapped to Recursion Depth)
Coordinate System: Cartesian
Max Depth: 14 (Batch Render), 12 (Viewer)
Base Square Size: 100.0
Algorithm: Recursive Square Construction (45-45-90 Triangle)

System: 2D Fractal (Complex Dynamics)
Name: Mandelbrot Set
Color Map: magma (Mapped to Escape Time)
Coordinate System: Complex Plane
Domain: x=[-2.0, 0.5], y=[-1.25, 1.25]
Max Iterations: 512 (Batch Render), 256 (Viewer)
Equation: z_{n+1} = z_n^2 + c

System: 2D Fractal (Iterated Function System)
Name: Levy C Curve
Color Map: cool (Mapped to Path Index)
Coordinate System: Cartesian (Iterative)
Iterations: 18 (Batch Render), 16 (Viewer)
Algorithm: Iterative Triangle Construction

System: 2D Fractal (Complex Dynamics)
Name: Newton Fractal (Basins of Attraction for z^3 - 1)
Color Map: Custom RGB (Red, Green, Blue for Roots)
Coordinate System: Complex Plane
Domain: x=[-1.5, 1.5], y=[-1.5, 1.5]
Max Iterations: 50 (Batch), 30 (Viewer)
Equation: z_{n+1} = z_n - (z_n^3 - 1) / (3z_n^2)

tessellations

Tessellations are patterns formed by repeating geometric shapes to cover a surface completely without any gaps or overlaps.

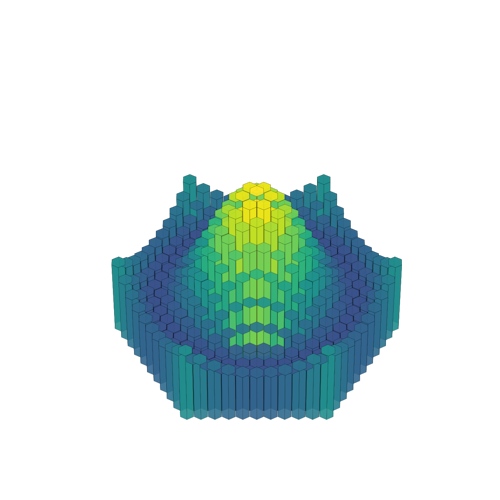System: 3D Tessellation
Name: Hexagonal Honeycomb Wave
Color Map: viridis (Mapped to Height)
Structure: Hexagonal Prisms
Grid Layers: 10
Radius: 1.0
Height Function: 5.0 + 3.0 * cos(distance / 4.0)

System: 2D Tessellation
Name: Cairo Pentagonal Tiling
Color Map: tab20 (Mapped to Tile Grouping)
Structure: Congruent Pentagons (4-fold symmetry groups)
Algorithm: Rotational Cluster Tiling
Render Style: Flat Polygons with Transparent Background

System: 3D Tessellation
Name: Voronoi Skyscraper City
Color Map: cool (Mapped to Height)
Structure: Random Voronoi Prisms
Seeds: 200 (Batch), 100 (Viewer)
Height Function: Gaussian Distribution (Central Peak)
Render Style: 3D Polygons with Transparent Background

System: 2D Tessellation
Name: Trihexagonal Tiling (Kagome Lattice)
Color Map: Set2 (Mapped to Shape Type: Hexagon, Tri-Up, Tri-Down)
Structure: Hexagons and Equilateral Triangles (3.6.3.6)
Algorithm: Grid-Based Unit Cell Placement
Render Style: Flat Polygons with Transparent Background

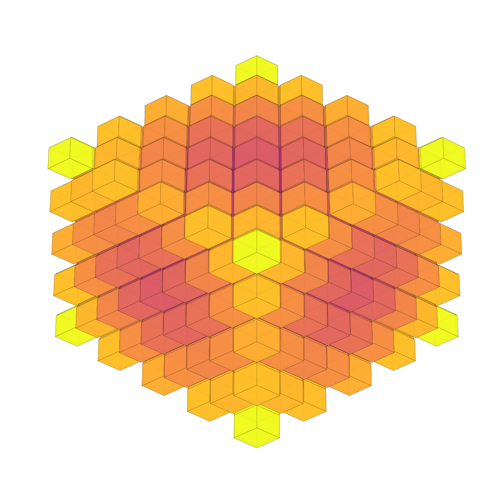System: 3D Tessellation (Space Filling)
Name: Rhombic Dodecahedron Honeycomb
Color Map: plasma (Mapped to Radial Distance)
Structure: Rhombic Dodecahedra on FCC Lattice
Grid Radius: 4 (Batch), 3 (Viewer)
Render Style: 3D Polygons with Transparent Background

System: 2D Tessellation (Aperiodic)
Name: Penrose P3 (Rhombus Tiling)
Color Map: coolwarm (Mapped to Rhomb Type: Thick/Thin)
Structure: Rhombi derived from Robinson Triangles
Generations: 7 (Batch), 5 (Viewer)
Algorithm: Deflation/Substitution

minimal surfaces

A minimal surface is a shape that naturally finds the most efficient way to stretch across a boundary, using the least amount of surface area possible.

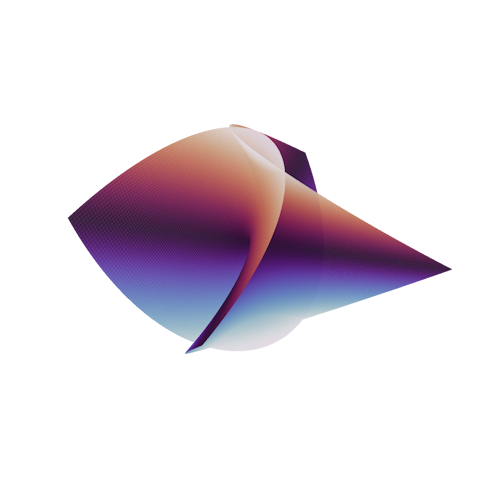System: Minimal Surface (Differential Geometry)
Name: Enneper's Surface
Color Map: twilight (Mapped to Z-Height)
Coordinate System: 3D Parametric Surface
Domain: u,v in [-2.0, 2.0]
Equations: x=u-u^3/3+uv^2; y=v-v^3/3+vu^2; z=u^2-v^2
Render Style: Surface Plot with Transparent Background

System: Minimal Surface (Ruled Surface)
Name: Helicoid
Color Map: plasma (Mapped to Z-Height)
Coordinate System: 3D Parametric Surface
Domain: u in [-2.0, 2.0], v in [-4pi, 4pi]
Equations: x=ucos(v); y=usin(v); z=c*v
Parameter c: 1.0

System: Minimal Surface (Surface of Revolution)
Name: Catenoid
Color Map: viridis (Mapped to Z-Height)
Coordinate System: 3D Parametric Surface
Domain: u in [0, 2pi], v in [-2.0, 2.0]
Equations: x=c*cosh(v/c)cos(u); y=ccosh(v/c)*sin(u); z=v
Parameter c: 1.0

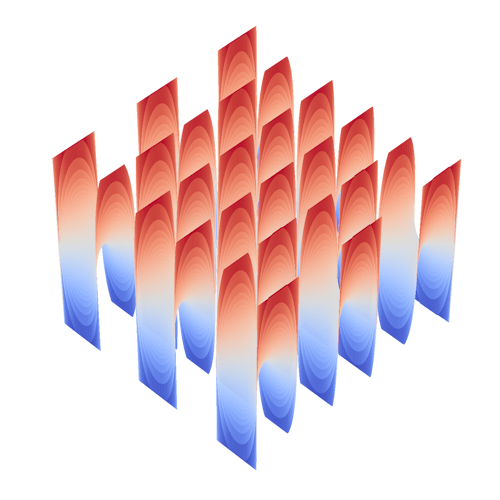System: Minimal Surface (Doubly Periodic)
Name: Scherk's First Surface
Color Map: coolwarm (Mapped to Z-Height)
Coordinate System: 3D Surface z(x,y)
Domain: x,y in [-2.5pi, 2.5pi]
Equation: z = ln(cos(x) / cos(y))

System: Minimal Surface
Name: Catalan's Surface
Color Map: winter (Mapped to Z-Height)
Coordinate System: 3D Parametric Surface
Domain: u in [0, 4pi], v in [-1.5, 1.5]
Equations: x=u-sin(u)cosh(v); y=1-cos(u)cosh(v); z=4sin(u/2)sinh(v/2)
Render Style: Surface Plot with Transparent Background

System: Minimal Surface (Non-orientable)
Name: Henneberg's Surface
Coordinate System: 3D Parametric Surface
Domain: u in [0, 0.8], v in [0, 2pi]
Parameters: None (Standard Form)
Equations: x = 2sinh(u)cos(v) - (2/3)sinh(3u)cos(3v)
y = 2sinh(u)sin(v) + (2/3)sinh(3u)sin(3v)
z = 2cosh(2u)cos(2v)

Art derived from mathematics - each piece emerges from precise algorithms, geometric relationships, and the elegant logic of numbers

attractors

parametric

fractals

tessellations

minimal surfaces

Script used to make this piece

Hash Info